Answer:
The magnitude of the pulling force is 20.66% of the gravitational force acting on the box
Step-by-step explanation:
Accelerated Motion
The net force exerted on a body is the (vector) sum of all forces applied to the body. The net force can be decomposed in its rectangular components and the dynamics of the body can be studied in each direction x,y separately.
Let's start off by calculating the acceleration the worker gives to the box when pulling it. The distance traveled by the box initially at rest in a time t at an acceleration a is given by
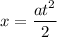
Solving for a
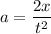
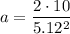

Now we analyze the geometric of the forces applied to the box. Please refer to the free body diagram provided below.
The forces in the y-axis must be in equilibrium since no movement takes place there, thus, being g the acceleration of gravity:
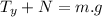
There Ty is the vertical component of the tension of the rope, N is the normal force, and m is the mass of the box
The decomposition of T gives us

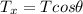
Solving the above equation for N
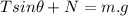
![N=m.g-Tsin\theta\text{..........[1]}](https://img.qammunity.org/2021/formulas/physics/college/vg0jbws107nohu44tek517slvpzpsi3lxo.png)
Now for the x-axis, there are two forces acting on the box, the x-component of the tension and the friction force Fr. Those forces are not equilibrated, thus acceleration is produced:

Recalling that
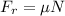
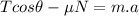
Replacing N from [1]
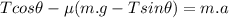
Operating
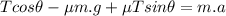
Solving for T
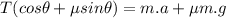
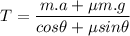
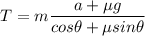
We don't know the value of m, thus we'll plug in the rest of the data
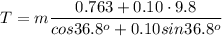
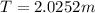
Dividing by the weight of the box m.g
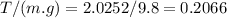
Thus, the magnitude of the pulling force is 20.66% of the gravitational force acting on the box