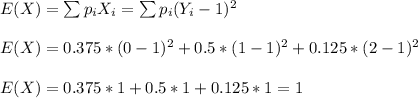Question

An unbiased die is tossed once. If the face of the die is and odd number, then an unbiased coin is tossed once. If the face of the die is an even number, then the coin is tossed twice. Let the random variable Y denote the number of heads obtained. (a) Determine the probability mass function (pmf) of Y. (b) Sketch the cumulative distribution function of Y. (c) Determine the expected values of Y and of (Y - 1)2

Answer 1

a) PMF

Explanation:

Answer 2

a) PMF

`P(Y=0) = 0.375\\\\P(Y=1)=0.5\\\\P(Y=2)=0.125`

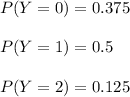
b) Cumulative distribution function

`P(Y\leq 0)=0.375\\\\P(Y\leq1)=0.875\\\\P(Y\leq2)=1`

c) E(Y)=0.75

E((Y-1)^2)=1

Explanation:

To write the pmf of Y we have to study the possible outcomes of this game. As this is a discrete game with no many possible outcomes, we can write them all one by one.

1) Event: The face of the die is an odd number and the coin is head (Y=1).

Probability:

`P_1=P(odd)*P(head)=0.5*0.5=0.25`

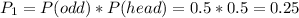
2) Event: The face of the die is an odd number and the coin is tail (Y=0).

Probability:

`P_2=P(odd)*P(tail)=0.5*0.5=0.25`

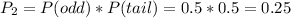
3) Event: The face of the die is an even number and the coin is tossed head two times (Y=2).

Probability:

`P_3=P(odd)*P(head)*P(head)=0.5*0.5*0.5=0.125`

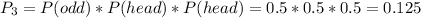
4) Event: The face of the die is an even number and the coin is tossed tail two times (Y=0).

Probability:

`P_4=P(odd)*P(tail)*P(tail)=0.5*0.5*0.5=0.125`

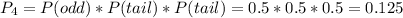
5) Event: The face of the die is an even number and the coin is tossed one time head and one time tail (Y=1). The probabilitiesare doubled because this could happen in two ways (first head or first tail).

Probability:

`P_5=P(odd)*(P(tail)*P(head)+P(head)*P(tail))\\\\P_5=0.5*(0.5*0.5+0.5*0.5)=0.25`

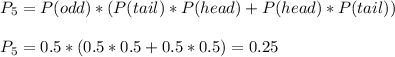
Then we have the pmf of Y as:

`P(Y=0) = P_2+P_4=0.25+0.125=0.375\\\\P(Y=1)=P_1+P_5=0.25+0.25=0.5\\\\P(Y=2)=P_3=0.125`

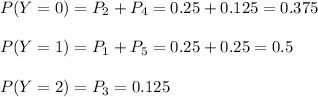
The cumulative distribution function of Y is

`P(Y\leq 0)=P(Y=0)=0.375\\\\P(Y\leq1)=P(Y\leq0)+P(Y=1)=0.375+0.5=0.875\\\\P(Y\leq2)=P(Y\leq1)+P(Y=2)=0.875+0.125=1`

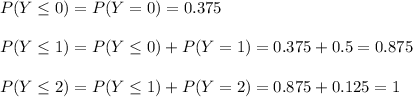
The expected value of Y is:

`E(Y)=\sum p_iY_i=0.375*0+0.5*1+0.125*2=0+0.5+0.25=0.75`

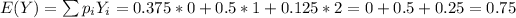
The expected value of X=(Y-1)² is:

`E(X)=\sum p_iX_i=\sum p_i(Y_i-1)^2\\\\E(X)=0.375*(0-1)^2+0.5*(1-1)^2+0.125*(2-1)^2\\\\E(X)=0.375*1+0.5*1+0.125*1=1`