Step-by-step explanation:
The given data is as follows.
Load on each wire = 11,100 N
Factor of safety (N) = 2
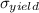 = 1030 MPa (150,000 Psi)
= 1030 MPa (150,000 Psi)
Now,
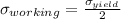
=
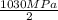
= 515 MPa (75,000 Psi)
So, we will calculate the diameter as follows.
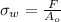
or,
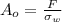
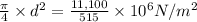
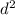 = 27.45
= 27.45
d = 5.24 mm
Thus, we can conclude that the minimum required wire diameter is 5.24 mm.