Question

The 25 lb block has an initial speed of v0 = 10 f t/s when it is midway between springs A and B. After striking spring B, it rebounds and slides across the horizontal plane toward spring A, etc. If the coefficient of kinetic friction between the plane and the block is µk = 0.4, determine the total distance traveled by the block before it comes to rest.

Answer 1

The total distance traveled by the block before it comes to rest is 3.517 ft.

Explanation :

Given that,

Weight of block = 25 lb

Initial speed = 10 ft/s

Coefficient of kinetic friction = 0.4

Spring constant
`k_(A)=10\ lb/in`

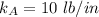
Spring constant
`k_(B)= 60\ lb/in`

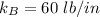
The kinetic energy of the system

`K.E_(1)=(1)/(2)mv_(0)^2`

`K.E_(1)=(1)/(2)*((W)/(g))v_(0)^2`

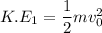
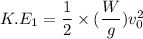
We need to calculate the frictional force

Using formula of frictional force

`F=\mu* W`

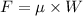
Put the value into the formula

`F=0.4*25`

`F=10\ N`

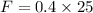
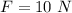
The potential work due to spring is zero because the block comes to rest.

We need to calculate the distance

Using work energy theorem

`K.E_(1)+\sum U=T_(2)`

`K.E_(1)-W_(f)-W_(s)=(1)/(2)k_(b)s^2`

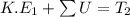
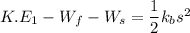
Put the value in the equation

`(1)/(2)*((W)/(g))v_(0)^2-10* (1+s_(1))-(1)/(2)k_(b)s_(3)^2=0`

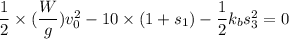
Here,
`s_(1)=s_(3)`

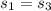
Put the value into the formula

`(1)/(2)*((25)/(32.2))*10^2-10+10s-(1)/(2)*60* s^2=0`

`38.81-10+10s_(1)-30s_(1)^2=0`

`28.81+10s-30s^2=0`

`s_(1)=0.827\ ft`

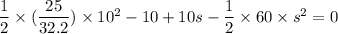
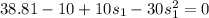
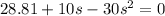
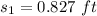
We need to calculate the distance s₂

Using work energy theorem

`K.E_(2)+\sum U=T_(3)`

`0+(1)/(2)k_(b)s_(3)^2-k_(A)(s_(1)+s_(2))=0`

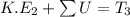
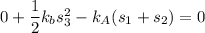
Put the value in to the formula

`(1)/(2)*60*(0.827)^3-10(0.827+s_(2))=0`

`16.9-8.27-10s_(2)=0`

`8.63-10s_(2)=0`

`s_(2)=(8.63)/(10)`

`s_(2)=0.863\ ft`

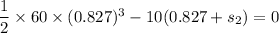
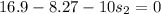
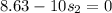
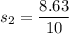
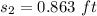
We need to calculate the total distance

`s=2s_(1)+s_(2)+1`

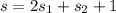
Put the value in the equation

`s=2*0.827+0.863+1`

`s=3.517\ ft`

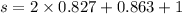
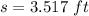
Hence, The total distance traveled by the block before it comes to rest is 3.517 ft.