Answer :
The total distance traveled by the block before it comes to rest is 3.517 ft.
Explanation :
Given that,
Weight of block = 25 lb
Initial speed = 10 ft/s
Coefficient of kinetic friction = 0.4
Spring constant
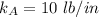
Spring constant
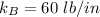
The kinetic energy of the system


We need to calculate the frictional force
Using formula of frictional force
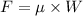
Put the value into the formula
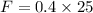
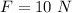
The potential work due to spring is zero because the block comes to rest.
We need to calculate the distance
Using work energy theorem
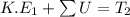

Put the value in the equation

Here,
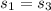
Put the value into the formula
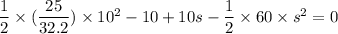

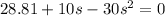
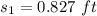
We need to calculate the distance s₂
Using work energy theorem
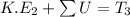
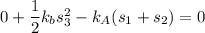
Put the value in to the formula
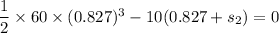
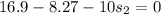
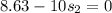

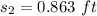
We need to calculate the total distance
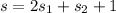
Put the value in the equation
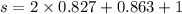
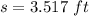
Hence, The total distance traveled by the block before it comes to rest is 3.517 ft.