Answer:
See step by step explanation.
Explanation:
Recall that given two integers a, b, a divides b if there exists an integer k such that b = ka.
Let a,b,d be integers, such that d>0.
a) Suppose that d divides a and d divides b. Then, there exists
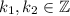 such that
such that
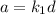 and
and
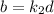 . Consider a+b and a-b. Replacing the previous equation, we have that
. Consider a+b and a-b. Replacing the previous equation, we have that

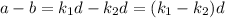
Since
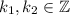 then
then
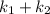 and
and
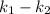 are both integers. Then, d divides both a+b and a-b.
are both integers. Then, d divides both a+b and a-b.
b) It is false. Let a = 7, b = 5. Then d = 2 divides a+b (12) and a-b (2) but neither 2 divides 7 nor 2 divides 5.