Presumably, both δ and ρ represent density of some object. Considering the context, ρ is likely a function of 3 variables, ρ = ρ(x, y, z). Then the mass of the sphere with the prescribed density δ(x, y, z) = k ρ(x, y, z) is
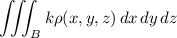
where B is the set

If you have all the details at hand, you can compute the integral by converting to spherical coordinates, substituting

The integral then transforms to
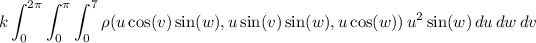
Without any additional information, there's not much more to say...