Answer:
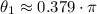 or
or
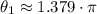 ,
,
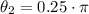 or
or

Explanation:
Let use the following substitution formula:
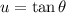
The trigonometric expression is converted into an algebraic one, a second-order polynomial:

Roots can be found by using the General Equation for Second-Order Polynomial:
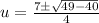
Roots are
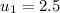 and
and
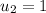 . As tangent function has a periodicity of
. As tangent function has a periodicity of
 , solutions of
, solutions of
 and
and
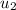 belong to first and third quadrants. Then, angles can be easily found by using inverse trigonometric functions:
belong to first and third quadrants. Then, angles can be easily found by using inverse trigonometric functions:
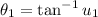
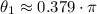 or
or
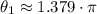
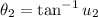
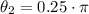 or
or
