Question

The edge of a cube was found to be 30 cm with a possible error in measurement of 0.2 cm. Use differentials to estimate the maximum possible error, relative error, and percentage error in computing the volume of the cube and the surface area of the cube. (Round your answers to four decimal places.) (a) the volume of the cube

Answer 1

Maximum volume error = ±540 cm³

Relative error = 0.02

Percentage error = 2%

Explanation:

Relative error : The ratio of volume error to the total volume.

Percentage error: The product of relative error and 100.

The volume of a cube is =
`side^3`

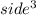
v =x³

Differentiate with respect to x

`(dv)/(dx) = 3x^2`

`\Rightarrow dv = 3x^2 dx`

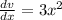
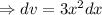
Here are x = 30 cm and dx= ±0.2 cm

∴ dv = 3×(30 cm)² (±0.2 cm)

=±540 cm³

The volume of the cube = 30³ cm ³ = 27,000 cm³

Then the relative error

`=(dv)/(v)`

`=(540 cm^3)/(27,000 cm^3)`

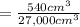
= 0.02.

The percentage error

= (0.02×100)

=2%