Answer:
Maximum volume error = ±540 cm³
Relative error = 0.02
Percentage error = 2%
Explanation:
Relative error : The ratio of volume error to the total volume.
Percentage error: The product of relative error and 100.
The volume of a cube is =
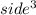
v =x³
Differentiate with respect to x
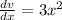
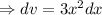
Here are x = 30 cm and dx= ±0.2 cm
∴ dv = 3×(30 cm)² (±0.2 cm)
=±540 cm³
The volume of the cube = 30³ cm ³ = 27,000 cm³
Then the relative error
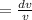
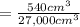
= 0.02.
The percentage error
= (0.02×100)
=2%