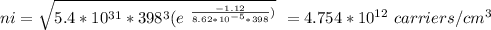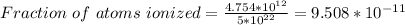Question

Find values of the intrinsic carrier concentration n for silicon at –70° 0° 20° C, 100° C, and C. At 125° each temperature, what fraction of the atoms is ionized?

Answer 1

Part (i) at –70° C, intrinsic carrier concentration of silicon is 2.865 x 10⁵ carriers/cm³ and fraction of the atoms ionized is 5.37 x 10⁻¹⁸

Part (ii) at 0° C, intrinsic carrier concentration of silicon is 1.533 x 10⁹ carriers/cm³ and fraction of the atoms ionized is 3.067 x 10⁻¹⁴

Part (iii) at 20° C, intrinsic carrier concentration of silicon is 8.652 x 10⁹ carriers/cm³ and fraction of the atoms ionized is 1.731 x 10⁻¹³

Part (iv) at 100° C, intrinsic carrier concentration of silicon is 1.444 x 10¹² carriers/cm³ and fraction of the atoms ionized is 2.889 x 10⁻¹¹

Part (iv) at 125° C, intrinsic carrier concentration of silicon is 4.754 x 10¹² carriers/cm³ and fraction of the atoms ionized is 9.508 x 10⁻¹¹

Step-by-step explanation:

`ni^2 = BT^3(e^{(-E_g)/(KT)})\\\\ni = \sqrt{ BT^3(e^{(-E_g)/(KT)})}`

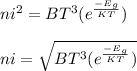
where;

B = 5.4 x 10⁻³¹

Eg = 1.12 ev

K = 8.62 x 10⁻⁵ eV/K

T = (273 + ⁰C) K

Number of atoms in silicon crystal = 5 x 10²² atoms/cm³

Part (i) For –70° C, T = (273 -70 ⁰C)K = 203 K

`ni = \sqrt{ 5.4*10^(31)*203^3(e^ \ {(-1.12)/(8.62*10^(-5)*203)})}} \ =2.685*10^5 \ carriers/cm^3`

`Fraction \ of \ atoms \ ionized = (2.685*10^5)/(5 *10^(22)) = 5.370 *10^(-18)`

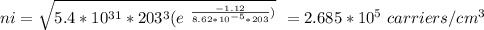
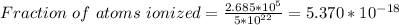
Part (ii) For 0° C, T = (273 +0 ⁰C)K = 273 K

`ni = \sqrt{ 5.4*10^(31)*273^3(e^ \ {(-1.12)/(8.62*10^(-5)*273)})}} \ =1.533*10^9 \ carriers/cm^3`

`Fraction \ of \ atoms \ ionized = (1.533*10^9)/(5 *10^(22)) = 3.067 *10^(-14)`

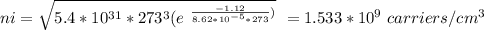
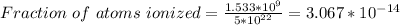
Part (iii) For 20° C, T = (273 + 20 ⁰C)K = 293 K

`ni = \sqrt{ 5.4*10^(31)*293^3(e^ \ {(-1.12)/(8.62*10^(-5)*293)})}} \ =8.652*10^9 \ carriers/cm^3`

`Fraction \ of \ atoms \ ionized = (8.652*10^9)/(5 *10^(22)) = 1.731 *10^(-13)`

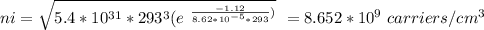
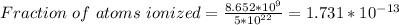
Part (iv) For 100° C, T = (273 + 100 ⁰C)K = 373 K

`ni = \sqrt{ 5.4*10^(31)*373^3(e^ \ {(-1.12)/(8.62*10^(-5)*373)})}} \ =1.444*10^(12) \ carriers/cm^3`

`Fraction \ of \ atoms \ ionized = (1.444*10^(12))/(5 *10^(22)) = 2.889 *10^(-11)`

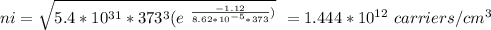
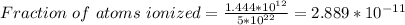
Part (v) For 125° C, T = (273 + 125 ⁰C)K = 398 K

`ni = \sqrt{ 5.4*10^(31)*398^3(e^ \ {(-1.12)/(8.62*10^(-5)*398)})}} \ =4.754*10^(12) \ carriers/cm^3`

`Fraction \ of \ atoms \ ionized = (4.754*10^(12))/(5 *10^(22)) = 9.508 *10^(-11)`