Answer:
The rate of change of the radius is 0.0066 cm/s when the radius is 11 cm.
Explanation:
The change in volume is according to the inflow of air, that has a rate of 10 cm3/s.
The volume of the sphere can be defined as:
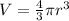
To calculate the rate of change of the radius (dr/dt), we have to derive the last expression.
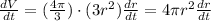
Then we have an expression for dr/dt:
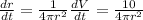
For r = 11 cm, we have:
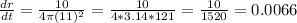
The rate of change of the radius is 0.0066 cm/s when the radius is 11 cm.