Question

Blowing Soap Bubbles Carlos is blowing air into a spherical soap bubble at the rate of 10 cm3/sec. How fast is the radius of the bubble changing when the radius is 11 cm? (Round your answer to four decimal places.)

Answer 1

The rate of change of the radius is 0.0066 cm/s when the radius is 11 cm.

Explanation:

The change in volume is according to the inflow of air, that has a rate of 10 cm3/s.

The volume of the sphere can be defined as:

`V=(4)/(3) \pi r^3`

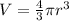
To calculate the rate of change of the radius (dr/dt), we have to derive the last expression.

`(dV)/(dt)=((4\pi)/(3))\cdot (3r^2)(dr)/(dt)=4\pi r^2(dr)/(dt)`

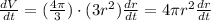
Then we have an expression for dr/dt:

`(dr)/(dt)=(1)/(4\pi r^2) (dV)/(dt)=(10)/(4\pi r^2)`

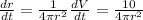
For r = 11 cm, we have:

`(dr)/(dt)=(10)/(4\pi (11)^2)=(10)/(4*3.14*121) =(10)/(1520)=0.0066`

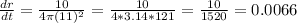
The rate of change of the radius is 0.0066 cm/s when the radius is 11 cm.