Question

The auto parts department of an automotive dealership sends out a mean of 5.2 special orders daily. What is the probability that, for any day, the number of special orders sent out will be exactly 4?

Answer 1

16.81% probability that, for any day, the number of special orders sent out will be exactly 4

Explanation:

The only information that we have is a mean during an interval. So we use the Poisson distribution solve this question.

We have that the probability of exactly x events is given by the following formula:

`P(X = x) = (e^(-\mu)*(\mu)^(x))/(x!)`

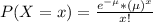
In which
`\mu` is the mean.

The auto parts department of an automotive dealership sends out a mean of 5.2 special orders daily.

This means that
`\mu = 5.2`

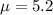
What is the probability that, for any day, the number of special orders sent out will be exactly 4?

This is P(X = 4).

`P(X = x) = (e^(-\mu)*(\mu)^(x))/(x!)`

`P(X = 4) = (e^(-5.2)*(5.2)^(4))/(4!) = 0.1681`

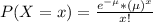
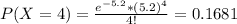
16.81% probability that, for any day, the number of special orders sent out will be exactly 4