Question

What is the product? 6 (x squared minus 1) times StartFraction 6 x minus 1 Over 6 (x + 1) EndFraction 6(x – 1)2 6(x2 – 1) (x + 1)(6x – 1) (x – 1)(6x – 1)

Answer 1

D on edge

Step-by-step explanation:

Answer 2

Option D:
`(6x-1)(x-1)` is the product of the expression

Step-by-step explanation:

The expression is
`6(x^(2) -1)*(6x-1)/(6(x+1))`

We need to determine the product of the expression.

To determine the product of the expression, we need to simplify the given expression.

Thus, we have,

`6(x^(2) -1^2)*(6x-1)/(6(x+1))`

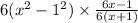
The term
`(x^(2) -1^2)` is of the form
`a^2-b^2`

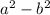
Now, we shall use the identity,
`a^2-b^2=(a+b)(a-b)`

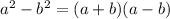
Hence, we have,

`6(x+1)(x-1)*(6(x-1))/(6(x+1))`

Multiplying the terms and cancelling the common terms, we get,

`(x-1)*({6x-1})`

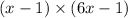
Hence, the product of the given expression is
`(6x-1)(x-1)`

Therefore, Option D is the correct answer.