Question

A simple generator has a square armature 5.0 cm on a side. The armature has 95 turns of 0.59-mm-diameter copper wire and rotates in a 0.800-T magnetic field. The generator is used to power a light bulb rated at 12.0 V and 25.0 W.

At what rate should the generator rotate to provide 12.0 V to the bulb? Consider the resistance of the wire on the armature.

Answer 1

`25.39Hz`

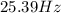
Step-by-step explanation:

#First, we need to determine the actual emf required. The generator's internal resistance will cause a voltage drop inside the generator/

Internal resistance is defined using the formula:

`R=\rho L/A\\\rho=1.68*10^-^8 \Omega m\\L=0.050m*4* 60=12.0m\\A=\pi r^2=\pi d^2/4=\pi(0.00059m)^2/4=2.734*10^-^7m^2\\\\R=(1.68*10^-^8 \Omega \ m* 12.0m)/2.734*10^-^7m^2\\=0.7374\ \Omega`

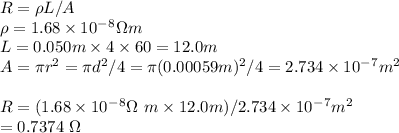
#The bulb is rated 12.0V,25.0W

Current,
`I=25.0W/12.0V=2.083A`

Therefore, the voltage drop in the generator is calculated as:

`2.083A*0.7374\Omega=1.5360V`

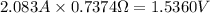
Actual EMF required is thus 1.536V+12.0V=13.536V

#peak voltage is
`13.536V\sqrt 2=19.143V`

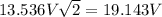
#For a generator, by Faraday's Law

`E_m_a_x=NBA\ \omega\\19.143=60* 0.800T* (0.05m)^2\ \omega\\\\\omega=159.525rad/s`

`f=\omega/2\pi\\=159.525/2\pi=25.39Hz`

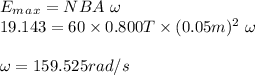
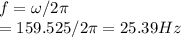
#The rate of the generator is 25.39Hz