Answer:
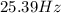
Step-by-step explanation:
#First, we need to determine the actual emf required. The generator's internal resistance will cause a voltage drop inside the generator/
Internal resistance is defined using the formula:
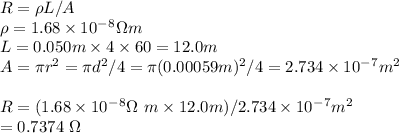
#The bulb is rated 12.0V,25.0W
Current,
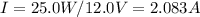
Therefore, the voltage drop in the generator is calculated as:
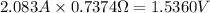
Actual EMF required is thus 1.536V+12.0V=13.536V
#peak voltage is
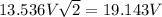
#For a generator, by Faraday's Law
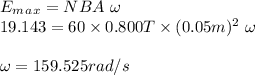
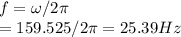
#The rate of the generator is 25.39Hz