Answer:
The probability that a car battery lasts more than 36 months is 0.4066.
Explanation:
Let X = the useful life of a particular car battery.
The decay parameter is, λ = 0.025.
The random variable X follows an Exponential distribution with parameter λ = 0.025.
The probability density function of X is:

Compute the probability that a car battery lasts more than 36 months as follows:


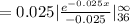
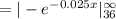
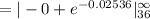
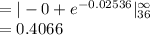
Thus, the probability that a car battery lasts more than 36 months is 0.4066.