Answer:
a)
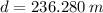 , b)
, b)
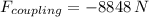 The real force has the opposite direction.
The real force has the opposite direction.
Step-by-step explanation:
a) Let assume that train moves on the horizontal ground. An equation for the distance travelled by the train is modelled after the Principle of Energy Conservation and Work-Energy Theorem:
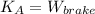
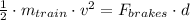
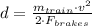
![d = ((51000\,kg)\cdot [(90\,(km)/(h) )\cdot ((1000\,m)/(1\,km) )\cdot ((1\,h)/(3600\,s) )]^(2))/(2\cdot (82000\,N))](https://img.qammunity.org/2021/formulas/engineering/college/b54edxlinyzeqgcdukl4nhmejs57azawqe.png)

b) The acceleration experimented by both trains are:

![a = -([(90\,(km)/(h) )\cdot ((1000\,m)/(1\,km) )\cdot ((1\,h)/(3600\,s))]^(2))/(2\cdot (194.360\,m))](https://img.qammunity.org/2021/formulas/engineering/college/evgnpmfsbfewvtfo91208he6p1wkzm2yl9.png)
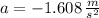
The coupling force in the car A can derived of the following equation of equilibrium:
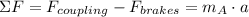
The coupling force between cars is:
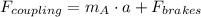
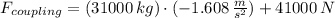
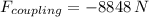
The real force has the opposite direction.