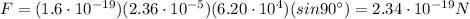Answer:
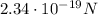
Step-by-step explanation:
The strength of the magnetic field produced by a current-carrying wire is:
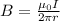
where:
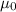 is the vacuum permeability
is the vacuum permeability
I is the current in the wire
r is the distance from the wire
In this case,
I = 5.20 A
r = 4.40 cm = 0.044 m
Therefore,

The direction of the field is along concentric circles centered in the wire.
The force exerted by a magnetic field on a moving charged particle is
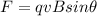
where
q is the charge
v is the velocity of the particle
 is the direction between v and B
is the direction between v and B
In this problem:
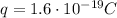 is the magnitude of the charge of the particle
is the magnitude of the charge of the particle
 is the velocity
is the velocity
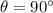 , because the electron is travelling towards the wire, so perpendicular to the lines of the magnetic field
, because the electron is travelling towards the wire, so perpendicular to the lines of the magnetic field
Therefore, the magnitude of the force is: