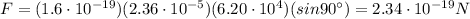Question

slader A long, straight wire carries a current of 5.20 AA. An electron is traveling in the vicinity of the wire. At the instant when the electron is 4.40 cmcm from the wire and traveling with a speed of 6.20×104 m/sm/s directly toward the wire, what is the magnitude of the force that the magnetic field of the current exerts on the electron?

Answer 1

`2.34\cdot 10^(-19)N`

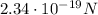
Step-by-step explanation:

The strength of the magnetic field produced by a current-carrying wire is:

`B=(\mu_0 I)/(2\pi r)`

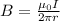
where:

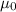`\mu_0` is the vacuum permeability

I is the current in the wire

r is the distance from the wire

In this case,

I = 5.20 A

r = 4.40 cm = 0.044 m

Therefore,

`B=((4\pi \cdot 10^(-7))(5.20))/(2\pi (0.044))=2.36\cdot 10^(-5) T`

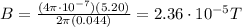
The direction of the field is along concentric circles centered in the wire.

The force exerted by a magnetic field on a moving charged particle is

`F=qvB sin \theta`

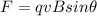
where

q is the charge

v is the velocity of the particle

`\theta` is the direction between v and B

In this problem:

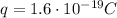`q=1.6\cdot 10^(-19)C` is the magnitude of the charge of the particle

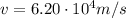`v=6.20\cdot 10^4 m/s` is the velocity

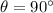`\theta=90^(\circ)`, because the electron is travelling towards the wire, so perpendicular to the lines of the magnetic field

Therefore, the magnitude of the force is:

`F=(1.6\cdot 10^(-19))(2.36\cdot 10^(-5))(6.20\cdot 10^4)(sin 90^(\circ))=2.34\cdot 10^(-19)N`