Answer:
Part 1) The domain of the quadratic function is the interval (-∞,∞)
Part 2) The range is the interval (-∞,1]
Explanation:
we have
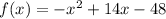
This is a quadratic equation (vertical parabola) open downward (the leading coefficient is negative)
step 1
Find the domain
The domain of a function is the set of all possible values of x
The domain of the quadratic function is the interval
(-∞,∞)
All real numbers
step 2
Find the range
The range of a function is the complete set of all possible resulting values of y, after we have substituted the domain.
we have a vertical parabola open downward
The vertex is a maximum
Let
(h,k) the vertex of the parabola
so
The range is the interval
(-∞,k]
Find the vertex
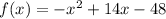
Factor -1 the leading coefficient
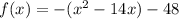
Complete the square
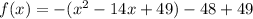
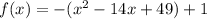
Rewrite as perfect squares
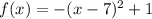
The vertex is the point (7,1)
therefore
The range is the interval
(-∞,1]