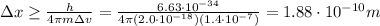Answer:
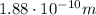
Step-by-step explanation:
Heisenberg's uncertainty principle states that it is not possible to know with infinite precision the position and the momentum of an object at the same time. Mathematically, this is written as:
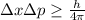
where:
 is the uncertainty on the position
is the uncertainty on the position
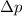 is the uncertainty on the momentum
is the uncertainty on the momentum
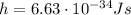 is the Planck's constant
is the Planck's constant
Since the momentum can be written as product of mass (m) and velocity:
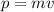
The uncertainty on the momentum can be written as (assuming the mass is known with infinite precision):
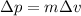
Therefore, the previous equation can be rewritten as:
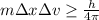
In this problem, we have:
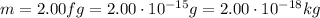 is the mass of the E.Coli
is the mass of the E.Coli
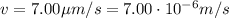 is the E.Coli velocity
is the E.Coli velocity
The uncertainty on the velocity is 2.00% of this value, so:

Therefore, if we now re-arrange the equation, we can find
 , the minimum uncertainty on the position of the bacterium:
, the minimum uncertainty on the position of the bacterium: