Answer:
1. 13.33 years
2. 11 years
3. 186 years
Step-by-step explanation:
Problem 1. Perry has an opportunity to invest with an APR of 5.25%.
Using the rule of 70, how long will it take his investment to double? (Round to the hundredths.)
Solution
The rule of 70 permits to make a quick estimation of the number of years an investment would double its value, depending on the annual percentage rate (APR).
The formula used for the rule of 70 is:

Substitute with APR = 5.25 and compute:
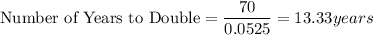
Problem 2. If you had a bank that offered 6.1% interest and compounded money 4 times a year, how many years would go by until you could turn $6000 into enough to buy a brand new car ($12,000)?
For this problem, you will want to guess and check until you find the right solution.
Solution
You have to use the formula for monthly compound interest:
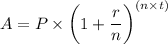
Where:
- A is the the value after adding the interests: $12,000
- P is the value invested: $6,000
- r is the APR: 6.1% = 0.061
- n is the number of times the interest is compounded per year: 4
- t is the number of years: your unknown
Substitute:
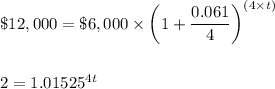
Guess and check until you find the right solution:
Your first educated guess may be using the rule of 70.
- Number of years = 70/6.1 = 11.48
Use t = 12 ⇒ 4t = 4(12) = 48
- 1.01525⁴⁸ = 2.067 . . . pretty close to 2
Use t = 11 to verify which is closer to 2:
t = 11 is closer because 2 - 1.946 = 0.054 and 2.067 - 2 = 0.067
Hence, the best calculation is 11 years.
Problem 3. How many years does it take for $100 to reach $1 million dollars? The rate is at 5% with it being compounded twice a year. Round to a whole year. Hint: You may want to start with numbers above 100 years!
Solution
Use the same formula for monthly compound interest:
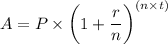
With:
- A: $100
- P: $1,000,000
- r: 5% = 0.05
- n: 2
- t: your unknown
Substitute:
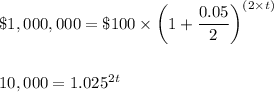
Guess and check until you find the right solution.
Start with t = 100 years:
- 1.025²⁰⁰ ≈ 140 . . . very far from 10,000
Try t = 200 years:
t = 150
t = 186
t = 187
9,756 is closer to 10,000 than 10,250, thus the answer is 186 years.