Question

NO LINKS!! Explain your answer (show the support by showing the changes in x and y on your table). If the relationship is linear, inverse, or exponential, write the equation.

#7 and #8​

Answer 1

Linear relationship: increasing or decreasing one variable will cause a corresponding increase or decrease in the other variable.

Inverse relationship: the value of one variable decreases as the value of the other variable increases.

Exponential relationship: a constant change in the independent variable (x) gives the same proportional change in the dependent variable (y)

Question 7

As the x-value increases (by one unit), the y-value decreases.

Therefore, this is an inverse relationship.

The y-values are calculated by dividing 16 by the x-value.

`\sf y=(16)/(x)`

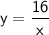
Question 8

As the x-value increases, the y-value increases.

The y-value increases by a factor of 2 for each x-value increase of 1 unit from 1 ≤ x ≤ 4 and 5 ≤ x ≤ 6.

`\sf y=2^x \ for \ 1\leq x\leq 4`

`\sf y=2^((x+3)) \ for \ 5\leq x \leq 6`

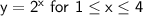
These are separate exponential relations for restricted domains.

So there doesn't appear to be one relationship for a non-restricted domain.

Answer 2

7. inverse relationship; equation: y = 16/x

8. no relationship; no equation

Explanation:

The attachment shows the support for the conclusions. The relationship can be chosen from those offered by looking at differences, ratios, or products of y-values for sequential x-values.

• linear: constant differences
• exponential: constant ratios
• inverse: constant products

__

7.

In the first problem, we note that the relationship between y-values varies inversely as the relationship between x-values: when x goes up by a factor of (n+1)/n, the value of y goes down by its inverse factor: n/(n+1). That same relationship is observed by noting that the product of x and y is a constant, 16.

relationship: inverse

y = 16/x

__

8.

As we looked at the table, we thought this might be an exponential function. Each y-value seemed to be twice the one before—until we got to x=5. As x went from 4 to 5, the y-value increased by a factor of 16, not 2. This means there is no simple relationship between x and y, and no simple equation that will describe the sequence of y-values.