Answer:
Linear relationship: increasing or decreasing one variable will cause a corresponding increase or decrease in the other variable.
Inverse relationship: the value of one variable decreases as the value of the other variable increases.
Exponential relationship: a constant change in the independent variable (x) gives the same proportional change in the dependent variable (y)
Question 7
As the x-value increases (by one unit), the y-value decreases.
Therefore, this is an inverse relationship.
The y-values are calculated by dividing 16 by the x-value.
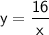
Question 8
As the x-value increases, the y-value increases.
The y-value increases by a factor of 2 for each x-value increase of 1 unit from 1 ≤ x ≤ 4 and 5 ≤ x ≤ 6.
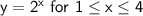

These are separate exponential relations for restricted domains.
So there doesn't appear to be one relationship for a non-restricted domain.