Answer:
9. a = -1
10. b = 20
Explanation:
The term "cross multiplying" is used to describe the appearance of the result of multiplying both sides of the equation by the product of the denominators. The result is the left numerator is multiplied by the right denominator, and the right numerator is multiplied by the left denominator. The property of equality that supports this is the multiplication property of equality, which tells you the values of the variables are unchanged if you multiply both sides by the same thing. That multiplier is chosen so that it cancels the denominators.
__
9.

__
10.
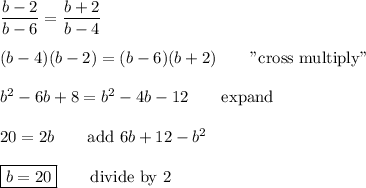
_____
Additional comments
Here are the answer checks:
9. (2(-1) -5)/(3(-1)-4) = (2(-1)-3)/(3(-1)-2) ⇒ -7/-7 = -5/-5 . . . yes
10. (10 -2)/(10 -6) = (10 +2)/(10 -4) ⇒ 8/4 = 12/6 . . . yes
__
Sometimes this method of solving the problem will result in extraneous solutions. Those will generally be values of the variable that make one or more of the denominators be zero. You must be careful to exclude those values from any possible solution set.