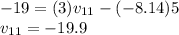Answer:
The velocity of the first mass is 19.9 m/s to the left
The velocity of the second mass is 8.14 m/s to the left
Step-by-step explanation:
In an elastic collision, both momentum and kinetic energy is conserved.
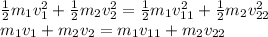
There is a lot of elaboration to solve these two equations, but substituting the values given in the question will ease the hard work.
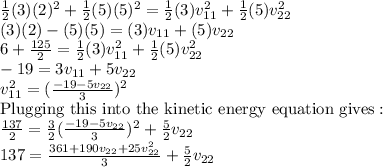
Rearranging the equations gives
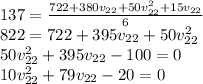
Solving this equation quadratically gives the velocity of the second mass:
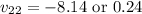
There are two roots to the quadratic equation, but we intuitively know that the bigger mass with the higher initial velocity will have the same direction after the collision.
Therefore, the final speed of the second mass is 8.14 m/s to the left.
Now, it is easy to calculate the velocity of the first mass.