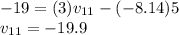Question

Suppose two masses labelled m1 and m2, are speeding toward each other at time t=0s. The first mass 1 has a mass and speed has values of m1=3 kg and v1,i= 2 m/s (to the right). Mass 2 has a mass and speed of m2 = 5kg with an initial speed of v2,I = 5 m/s (to the left). Then at some time t there is an elastic collision between the two masses. What is the final speed and direction of m1 and m2 after the collision.

Answer 1

The velocity of the first mass is 19.9 m/s to the left

The velocity of the second mass is 8.14 m/s to the left

Step-by-step explanation:

In an elastic collision, both momentum and kinetic energy is conserved.

`(1)/(2)m_1v_1^2 + (1)/(2)m_2v_2^2 = (1)/(2)m_1v_(11)^2 + (1)/(2)m_2v_(22)^2\\m_1v_1 + m_2v_2 = m_1 v_(11) + m_2 v_(22)`

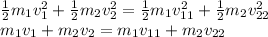
There is a lot of elaboration to solve these two equations, but substituting the values given in the question will ease the hard work.

`(1)/(2)(3)(2)^2 + (1)/(2)(5)(5)^2 = (1)/(2)(3)v_(11)^2 + (1)/(2)(5)v_(22)^2\\(3)(2) - (5)(5) = (3) v_(11) + (5) v_(22)\\6 + (125)/(2) = (1)/(2)(3)v_(11)^2 + (1)/(2)(5)v_(22)^2\\-19 = 3 v_(11) + 5 v_(22)\\v_(11)^2 = ((-19 - 5v_(22))/(3))^2\\{\rm Plugging ~this ~into~the~kinetic~energy~equation~gives:}\\(137)/(2) = (3)/(2)((-19-5v_(22))/(3))^2 + (5)/(2)v_(22)\\137 = (361 + 190v_(22) + 25v_(22)^2)/(3) + (5)/(2)v_(22)`

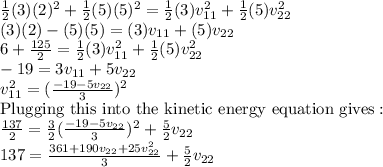
Rearranging the equations gives

`137 = (722 + 380v_(22) + 50v_(22)^2 + 15v_(22))/(6)\\822 = 722 + 395v_(22) + 50v_(22)^2\\50v_(22)^2 + 395v_(22) - 100 = 0\\10v_(22)^2 + 79v_(22) - 20 = 0`

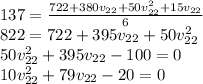
Solving this equation quadratically gives the velocity of the second mass:

`v_(22) = -8.14~{\rm or}~0.24`

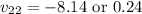
There are two roots to the quadratic equation, but we intuitively know that the bigger mass with the higher initial velocity will have the same direction after the collision.

Therefore, the final speed of the second mass is 8.14 m/s to the left.

Now, it is easy to calculate the velocity of the first mass.

`-19 = (3)v_(11) -(-8.14)5\\ v_(11) = -19.9`