Answer:
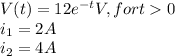
a)
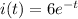
b)

c)
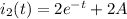
d) 36 joules
e) 48 joules
f)18 joules
g) Yes, they are equal
Step-by-step explanation:
a) - e) integrate from the circuit diagram
f) Trapped energy by the indicators:
L₁ = 6 joules
L₂ = 12 joules
g) The energy delivered to the Blackbox = Indicator Initial Energy - Inductor Trapped Energy
This translates to 36 = 54 - 18
36 = 36
Therefore, as the left hand side is equal to the right hand side, they are equal.