Question

Use the given data to find the minimumsample size required to estimate a population proportion or percentage. You are the operations manager for American Airlines and you areconsidering a higher fare level for passengers in aisle seats. You want to estimate the percentageof passengers who now prefer aisle seats. How many randomly selected air passengers mustyou survey? Assume that you want to be 95% confident that the sample percentage is within2.5 percentage points of the true population percentage. Assume that a prior survey suggests that about 38% of air passengers prefer an aisle seat(based on a 3M Privacy Filters survey).

Answer 1

The minimum sample size required is 1449.

Explanation:

The (1 - α) % confidence interval for population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

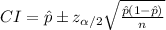
The margin of error in this interval is:

`MOE= z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

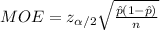
Given:

`\hat p = p = 0.38\\MOE=2.5\%\\z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

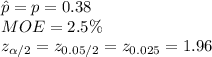
*Use the z-table for the critical value.

Compute the value of n as follows:

`MOE= z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}\\n=(z_(\alpha/2)^(2)* \hat p(1-\hat p))/(MOE^(2))\\=(1.96^(2)*0.38*(1-0.38))/(0.0025^(2))\\=1448.129536\\\approx1449`

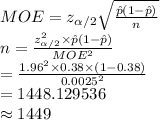
Thus, the minimum sample size required is 1449.