Answer:
The minimum sample size required is 1449.
Explanation:
The (1 - α) % confidence interval for population proportion is:
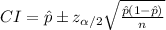
The margin of error in this interval is:
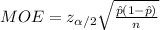
Given:
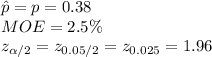
*Use the z-table for the critical value.
Compute the value of n as follows:
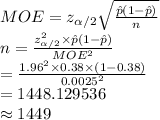
Thus, the minimum sample size required is 1449.