Question

A rectangular field with one side along a river is to be fenced. Suppose that no fence is needed along the river, the fence on the side opposite the river costs $40 per foot, and the fence on the other sides costs $10 per foot. If the field must contain 28,800 square feet, what dimensions will minimize costs?

Answer 1

Side opposite the river = 120 ft

Other sides = 240 ft

Step-by-step explanation:

Let 'R' denote the length of fence opposite to the river and 'L' denote the length of the other two sides.

The cost as a function of R is:

`L*R = 28,800\\L=(28,800)/(R)\\ C = 40R+10*2*(28,800)/(R) \\C(R) = 40R+576,000R^(-1)`

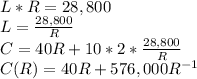
The value of R for which the derivate of the cost function is zero is the length that minimizes cost:

`C'(R) =0= 40 -576,000R^(-2)\\R=\sqrt{(576,000)/(40)}\\R=120\ ft\\`

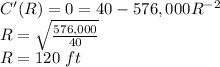
If R is 120 ft, then the value of L is:

`L = (28,800)/(120)\\L=240\ ft`

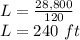
The dimensions that will minimize costs are:

Side opposite the river = 120 ft

Other sides = 240 ft