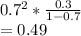Answer:
Step-by-step explanation:
Given that the probability of a customer arrival at a grocery service counter in any one second is equal to 0.3
Assume that customers arrive in a random stream, so an arrival in any one second is independent of all others.
i.e. X the no of customers arriving is binomial with p = 0.3 and q = 1-0.3 =0.7
a) the probability that the first arrival will occur during the third one-second interval.
= Prob that customer did not arrive in first 2 seconds * prob customer arrive in 3rd sec
=
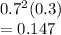
b) the probability that the first arrival will not occur until at least the third one-second interval.
Prob that customer did not arrive in first two seconds *(Prob customer arrives in 3rd or 4th or 5th.....)
=
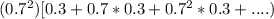
The term inside bracket is a geometric infinite progression with common ratio - 0.7 <1
Hence the series converges
Prob =