Question

The expected number of typographical errors on any page of a certain magazine is 0.2. What is the probability that a certain page you read contains a total of 2 or more typographical errors

Answer 1

The probability of 2 or more errors is 0.018.

Explanation:

Let X = number of typographical errors on a page of a certain magazine.

The expected number of errors is, λ = 0.2.

The random variable X follows a Poisson distribution with parameter λ = 0.2.

The probability mass function of X is:

`P(X=x)=(e^(-0.2)0.2^(x))/(x!);\ x=0,1,2,3...`

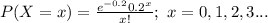
Compute the probability of 2 or more errors as follows:

P (X ≥ 2) = 1 - P (X < 2)

= 1 - P (X = 0) - P (X = 1)

`=1-(e^(-0.2)0.2^(0))/(0!)-(e^(-0.2)0.2^(1))/(1!)\\=1-0.81873-0.16375\\=0.01752\\\approx0.018`

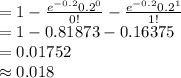
Thus, the probability of 2 or more errors is 0.018.