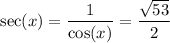In quadrant IV, cosine is positive and sine is negative. This means that
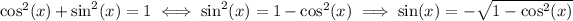
The cotangent is defined as the ratio between the cosine and sine:
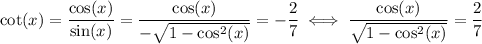
So, we have the following equation:
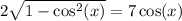
Squaring both sides yields
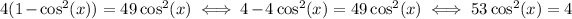
The solution to this equation would be
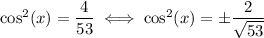
But we know that the cosine has to be positive, so we have
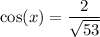
And
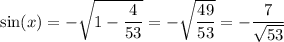
Finally, the secant is the inverse of the cosine, so it's