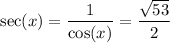Question

Let 0 be an angle in quadrant IV such that cot 0 = -2/7. Find the exact values of sin 0 and sec 0

Answer 1

In quadrant IV, cosine is positive and sine is negative. This means that

`\cos^2(x)+\sin^2(x)=1 \iff \sin^2(x)=1-\cos^2(x) \implies \sin(x)=-\sqrt{1-\cos^2(x)`

The cotangent is defined as the ratio between the cosine and sine:

`\cot(x)=(\cos(x))/(\sin(x))=(\cos(x))/(-√(1-\cos^2(x)))=-(2)/(7)\iff (\cos(x))/(√(1-\cos^2(x)))=(2)/(7)`

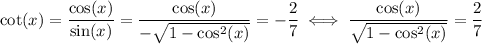
So, we have the following equation:

`2√(1-\cos^2(x))=7\cos(x)`

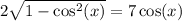
Squaring both sides yields

`4(1-\cos^2(x))=49\cos^2(x) \iff 4-4\cos^2(x)=49\cos^2(x)\iff 53\cos^2(x)=4`

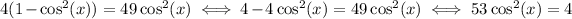
The solution to this equation would be

`\cos^2(x)=(4)/(53)\iff \cos^2(x)=\pm(2)/(√(53))`

But we know that the cosine has to be positive, so we have

`\cos(x)=(2)/(√(53))`

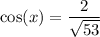
And

`\sin(x)=-\sqrt{1-(4)/(53)}=-\sqrt{(49)/(53)}=-(7)/(√(53))`

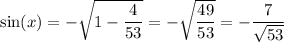
Finally, the secant is the inverse of the cosine, so it's

`\sec(x)=(1)/(\cos(x))=(√(53))/(2)`