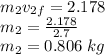Question

A ball of mass 0.220 kg that is moving with a speed of 6.3 m/s collides head-on and elastically with another ball initially at rest. Immediately after the collision, the incoming ball bounces backward with a speed of 3.6 m/s. (Assume the positive direction is forward.)

(a) Calculate the velocity of the target ball after the collision.
(b) Calculate the mass of the target ball.

Answer 1

(a) Velocity of target is 2.7 m/s.

(b) Mass of target is 0.807 kg.

Step-by-step explanation:

Mass of ball
`m_(1)=0.22\;kg`

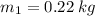
initial speed of the ball
`v_(1i)=6.3\;m/s`

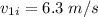
Final speed of the ball
`v_(2f)=-3.6\;m/s`

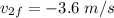
Part (a) The second ball is initially at rest. So, by the conservation of momentum,

`p_(i)=p_(f)\\m_(1)v_(1i)+m_(2)v_(2i)=m_(1)v_(1f)+m_(2)v_(2f)\\0.22*6.3+m_(2)* 0=0.22*(-3.6)+m_2v_(2f)\\m_2v_(2f)=2.178\:\:\:\:\;\;\;\;\;\;\;\;\;\; ...(1)`

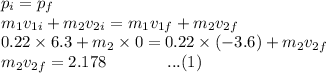
Now, the velocity of approach is equal to the velocity of separation,

`v_(1i)-v_(2i)=v_(2f)-v_(1f)\\6.3-0=v_(2f)-(-3.6)\\v_(2f)=2.7\;m/s`

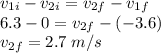
Part (b): From equation (1),

`m_2v_(2f)=2.178\\m_2=(2.178)/(2.7)\\m_2=0.806\;kg`