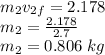Answer:
(a) Velocity of target is 2.7 m/s.
(b) Mass of target is 0.807 kg.
Step-by-step explanation:
Mass of ball
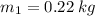
initial speed of the ball
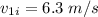
Final speed of the ball
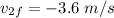
Part (a) The second ball is initially at rest. So, by the conservation of momentum,
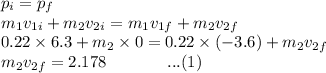
Now, the velocity of approach is equal to the velocity of separation,

Part (b): From equation (1),