Question

The number of chips in a bag is normally distributed with a mean of 74 and a standard deviation of 4. Approximately what percent of bags contain between 62 and 86 chips

Answer 1

99.73% of bags contain between 62 and 86 chips .

Explanation:

We are given that the number of chips in a bag is normally distributed with a mean of 74 and a standard deviation of 4.

Let X = percent of bags containing chips

So, X ~ N(
`\mu = 74 , \sigma^(2)=4^(2)`)

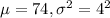The standard normal z score distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

So, percent of bags contain between 62 and 86 chips is given by;

P(62 < X < 86) = P(X < 86) - P(X <= 62)

P(X < 86) = P(
`(X-\mu)/(\sigma)` <
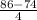`(86-74)/(4)` ) = P(Z < 3) = 0.99865 {using z table}

P(X <= 62) = P(
`(X-\mu)/(\sigma)` <=
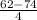`(62-74)/(4)` ) = P(Z <= -3) = 1 - P(Z < 3)= 1 - 0.99865 = 0.00135

So, P(62 < X < 86) = 0.99865 - 0.00135 = 0.9973 or 99.73%

Therefore, 99.73% of bags contain between 62 and 86 chips .