Question

(1 point) Consider the function f(x)=−x3+2x2+2x+1 Find the average slope of this function on the interval (−2,6). equation editor By the Mean Value Theorem, we know there exists a c in the open interval (−2,6) such that f′(c) is equal to this mean slope. Find the value of c in the interval which works.

Answer 1

Explanation:

Given is a function

`f(x)=-x^3+2x^2+2x+1`

`f(6) = -6^3+2(6^2)+2(6)+1\\=-131\\`

`f(-2) = -(-2)^3+2(-2)^2+2(-2)+1\\=13`

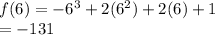
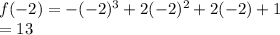
Average slope of this function is change of f(x) in (-2,6)/change of x in (-2,6)

=
`(-131-13)/(8) \\=-18`

By mean value theorem there exists a c such that f'(c) = -18

i.e.
`-3x^2+4x+2 =-8\\3x^2-4x-10 =0\\`

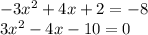
Using quadratic formula

x = 2.61, -1.277

Out of these only 2.61 lies in the given interval

c = 2.61