Answer:
The answer to the question is;
Based on their acceleration the rank of the satellites from largest to smallest is.
B >→ A >→ E >→ C >→ F >→ D.
Step-by-step explanation:
Acceleration is given by
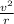
Therefore the acceleration for each of the satellite is given by
Satellite A)
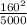 = 5.12 m/s²
= 5.12 m/s²
Satellite B)
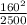 = 10.24 m/s²
= 10.24 m/s²
Satellite C)
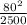 = 2.56 m/s²
= 2.56 m/s²
Satellite D)
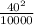 = 0.16 m/s²
= 0.16 m/s²
Satellite E)
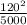 = 2.88 m/s²
= 2.88 m/s²
Satellite F)
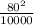 = 0.64 m/s²
= 0.64 m/s²
Therefore in order of decreasing acceleration, from largest to smallest we have
Satellite B) > Satellite A) >Satellite E) >Satellite C)>Satellite F)>Satellite D).