Question

Assignment 6 – Spring 2020 1. A hotel claims that 90% of its customers are very satisfied with its service. Suppose that a random sample of eight customers is chosen. a. What is the probability that seven customers are very satisfied? [P(X = 7)]? Round to four decimal places. (3 points)

Answer 1

P(X = 7) = 0.3826

Explanation:

We are given that a hotel claims that 90% of its customers are very satisfied with its service. A random sample of eight customers is chosen.

The Binomial probability distribution is given by;

`P(X=r) = \binom{n}{r}p^(r)(1-p)^(n-r) , x = 0,1,2,3,...`

where, n = number of trials (samples) taken = 8

r = number of success

p = proportion of customers that are satisfied with hotel's service,

i.e.; p = 0.90

Let = Number of customers that are very satisfied

So, Probability that seven customers are very satisfied = P(X = 7)

P(X = 7) =
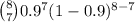
`\binom{8}{7}0.9^(7)(1-0.9)^(8-7)`

= 8 *
`0.9^(7) * 0.1^(1)` = 0.3826

Therefore, probability that seven customers are very satisfied is 0.3826.