Answer:
The wave speed would be increased by

Step-by-step explanation:
As the formula for the wave speed of string v when subjected to tension T is:
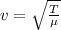
where μ is the string density (mass per length), which is constant for this case.
So when a string is subjected to tension 2T then
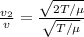

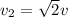
So the wave speed would be increased by
