Question

An isolated charged conducting sphere of radius 11.0 cm creates an electric field of 4.90 ✕ 104 N/C at a distance 20.0 cm from its center. (a) What is its surface charge density?

Answer 1

Complete Question:

An isolated, charged conducting sphere of radius 11.0 cm creates an electric field of 4.90×10⁴ N/C at a distance 20.0 cm from its center. (a) What is its surface charge density? (b) What is its capacitance?

Answer:

(a) 1.47 x 10⁻⁶ C/m² or 1.47 μC/m²

(b) 12.07 x 10⁻¹² F or 12.07 pF

Step-by-step explanation:

The surface charge density, σ, of a surface (sphere, in this case) of area A which has a charge Q uniformly distributed on it is given by;

σ =
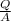`(Q)/(A)` -----------------(i)

Also, the electric field, E, due to the charge Q, at a distance r, from the center of the sphere to another point on the sphere is given as;

E = k x
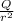`(Q)/(r^2)` --------------(ii)

Where;

k = Coulomb's constant = 8.99 x 10⁹Nm²/C²

(a) i. First calculate the charge on the sphere as follows;

From the question;

r = 20.0cm = 0.20m

E = 4.90 x 10⁴ N/C

Substitute these values into equation (ii) as follows;

4.90 x 10⁴ = 8.99 x 10⁹ x
`(Q)/(0.20^2)`

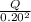
4.90 x 10⁴ = 8.99 x 10⁹ x
`(Q)/(0.04)`

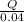
4.90 x 10⁴ = 224.75 x 10⁹ x Q

Q =
`(4.90*10^4)/(224.75*10^9)`

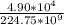
Q = 0.022 x 10⁻⁵

Q = 0.22 x 10⁻⁶ C

(a) ii. Also calculate the area A, of the sphere as follows;

A = 4π R²

Where;

R = radius of the sphere = 11.0cm = 0.11m

Substitute this value into equation above;

A = 4π (0.11)² [Take π = 3.142]

A = 4(3.142)(0.0121)

A = 0.15m²

(a) iii. Now calculate the surface charge density, of the sphere as follows;

Substitute the values of A and Q into equation (i) as follows;

σ =
`(0.22 * 10^(-6))/(0.15)`

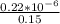
σ = 1.47 x 10⁻⁶C/m²

Therefore the surface charge density is 1.47 x 10⁻⁶C/m²

==============================================================

(b) The capacitance C, of an isolated charged sphere with radius R, is given by;

C = Aε₀ / R ----------------(iii)

Where;

R = 11.0cm = 0.11m

A = area of the sphere = 0.15m² [as calculated above]

ε₀ = permittivity of free space = 8.85 x 10⁻¹² C/Nm² [a known constant]

Substitute these values into equation (iii) as follows;

C = 0.15 x 8.85 x 10⁻¹² / 0.11

C = 12.07 x 10⁻¹²F

Therefore, the capacitance of the charged sphere is 12.07 x 10⁻¹²F

Answer 2

Surface charge density = 1.43 × 10⁶μC/m²

Step-by-step explanation:

surface charge density = Q /A_____(1)

where charge Q is the uniformly distributed on surface area A and d surface charge density σ

The electric field due to uniformly charge sphere of charge Q a distance r from the center of the sphere

`E = k(Q)/(r^2)`______(2)

where k is 8.988 × 10⁹N.m²C²

The surface area of the sphere is 4πR² ______(3)

The Capacitance is 4πε₀R

where ε₀ = 8.8542 × 10⁻¹²C/Nm² is a constant

Given that,

R = 11cm = 0.11m

E = 4.90 ✕ 10⁴ N/C

r = 20.0cm = 0.20m

substitute for Q in eqn(2) and for A in eqn(3)

surface charge density =
`(Er^2 )/(k(4\pi R^2)) \\((4.9 * 10^4)(0.20)^2)/(4\pi (8.988 * 10^9)(0.11)^2 )`

= 1.43 * 10⁶C/m²

Surface charge density = 1.43 μC/m²