Question

A baseball team has 4 ​pitchers, who only​ pitch, and 16 other​ players, all of whom can play any position other than pitcher. For​ Saturday's game, the coach has not yet determined which 9 players to use nor what the batting order will​ be, except that the pitcher will bat last. How many different batting orders may​ occur?

Answer 1

2,075,673,600 batting orders may occur.

Explanation:

The order of the first eight batters in the batting order is important. For example, if we exchange Jonathan Schoop with Adam Jones in the lineup, that is a different lineup. So we use the permutations formula to solve this problem.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

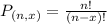
First 8 batters

8 players from a set of 16. So

`P_((16,8)) = (16!)/((16 - 8)!) = 518918400`

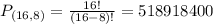
Last batter:

Any of the four pitchers.

How many different batting orders may​ occur?

4*518918400 = 2,075,673,600

2,075,673,600 batting orders may occur.