Question

This exercise illustrates that poor quality can affect schedules and costs. A manufacturing process has 100 customer orders to fill. Each order requires one component part that is purchased froma supplier. However, typically, 2% of the components are identifiedas defective, and the components can be assumed to beindependent.a)If the manufacturer stocks 100 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?b) If the manufacturer stocks 102 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?c) If the manufacturer stocks 105 components, what is theprobability that the 100 orders can be filled without reorderingcomponents?

Answer 1

(a) 0.1326

(b) 0.2732

(c) 0.0410

Explanation:

Let X = number of defective components.

The probability of X is, P (X) = p = 0.02.

The random variable X follows a Binomial distribution with parameters n and p. The probability mass function of a Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x);\ x=0,1,2,3,...`

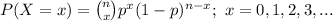
(a)

Compute the probability that the 100 orders can be filled without reordering components as follows:

n = 100

`P(X=0)={100\choose 0}0.02^(0)(1-0.02)^(100-0)=1*1*0.13262=0.1326`

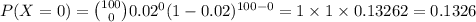
Thus, the probability that the 100 orders can be filled without reordering components is 0.1326.

(b)

Compute the probability that out of 102 orders 2 orders needs reordering as follows:

n = 102

`P(X=2)={102\choose 2}0.02^(2)(1-0.02)^(102-2)=5151*0.0004*0.13262=0.2732`

Thus, the probability that out of 102 orders 2 orders needs reordering is 0.2732.

(c)

Compute the probability that out of 105 orders 2 orders needs reordering as follows:

n = 105

`P(X=5)={105\choose 5}0.02^(5)(1-0.02)^(105-5)=96560646*0.0000000032*0.13262=0.0410`

Thus, the probability that out of 105 orders 5 orders needs reordering is 0.0410.