Answer:
k=1
P(12)=256
Explanation:
The model for population involving birth and death is given as:
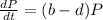
where b=birth rate and d=death rate.
If the birth and death rate are inversely proportional to
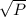
 where A and B are constants of variation.
where A and B are constants of variation.
Substituting b and d into our model
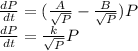 where A-B=k, another constant
where A-B=k, another constant
Simplifying using indices
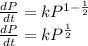
Next, we Separate Variables and Integrate both sides
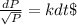

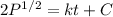 where C is the constant of integration
where C is the constant of integration
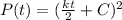
When t=0, P(t)=
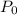 , C=
, C=
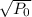
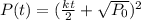 as required.
as required.
(b)If
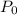 =100, t=6 months, P(t)=169
=100, t=6 months, P(t)=169
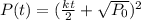

Since we have found the constant k, we can then calculate the population after 1 year. Note that we use 12 months since we used month earlier to get k.
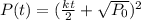
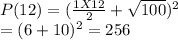
Therefore the population after a year is 256.