Answer:
The position s, velocity v, and acceleration a when t = 4s are 40m, 26m/s and 11m/s² respectively.
Step-by-step explanation:
The velocity, v, of the particle at any time, t, is given by;
v = 2 - 4t + 5
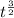 ----------(i)
----------(i)
Analysis 1: To get the position, s, of the particle at any time, t, we integrate equation (i) with respect to t as follows;
s = ∫ v dt
Substitute the value of v into the above as follows;
s = ∫ (2 - 4t + 5
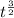 ) dt
) dt
s = 2t -
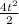 +
+

s = 2t -2t² + 2
 + c [c is the constant of integration] ------------(ii)
+ c [c is the constant of integration] ------------(ii)
According to the question;
when t = 0, s = 2m
Substitute these values into equation (ii) as follows;
2 = 2(0) -2(0)² + 2
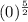 + c
+ c
2 = 0 - 0 - 0 + c
c = 2
Substitute the value of c = 2 back into equation (ii) as follows;
s = 2t -2t² + 2
 + 2 --------------------------------(iii)
+ 2 --------------------------------(iii)
Analysis 2: To get the acceleration, a, of the particle at any time, t, we differentiate equation (i) with respect to t as follows;
a =
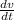
Substitute the value of v into the above as follows;
a =
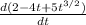
a = -4 +
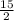
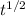 ----------------------------------(iv)
----------------------------------(iv)
Now;
(a) When t = 4s, the position s, of the particle is calculated by substituting t=4 into equation (iii) as follows;
s = 2(4) -2(4)² + 2(
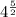 ) + 2
) + 2
s = 8 - 32 + 2(4)²°⁵
s = 8 - 32 + 2(32)
s = 8 - 32 + 64
s = 40m
(b) When t = 4s, the velocity v, of the particle is calculated by substituting t=4 into equation (i) as follows;
v = 2 - 4(4) + 5(
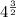 )
)
v = 2 - 16 + 5(4)¹°⁵
v = 2 - 16 + 5(8)
v = 2 - 16 + 40
v = 26m/s
(c) When t = 4s, the acceleration a, of the particle is calculated by substituting t = 4 into equation (iv) as follows;
a = -4 +
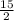 (
(
 )
)
a = -4 +
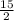 (2)
(2)
a = -4 + 15
a = 11m/s²
Therefore, the position s, velocity v, and acceleration a when t=4s are 40m, 26m/s and 11m/s² respectively.