Question

Triangle ADE is similar to triangle ABC. Which statement is TRUE concerning the slope of the line formed by the hypotenuse of each triangle? A) EA DE = CB AC B) DE EA = CB AC C) DE EA = AC CB D) EA DE = AC CB

Answer 1

b

Explanation:

took test

Answer 2

`B) (DE )/(EA) =(CB)/(AC)`

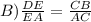
Explanation:

If ant two given triangles are SIMILAR, then they have equal corresponding angles and their corresponding sides are PROPORTIONAL.

For example: if Δ ABC ≈ Δ PQR, then

∠A = ∠P , ∠B = ∠Q and ∠C = ∠R

and
`(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)`

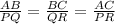
Now, here given: Δ ADE ≈ Δ ABC

Then by the SIMILAR postulate their corresponding angles are equal and their corresponding sides are Proportional.

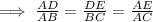`\implies (AD)/(AB) = (DE)/(BC) = (AE)/(AC)` ............. (1)

Consider from above:

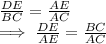`(DE)/(BC) = (AE)/(AC)\\\implies (DE)/(AE) = (BC)/(AC)` ............. (2)

Here, the given options are:

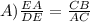`A) (EA )/(DE) =(CB)/(AC)` FALSE

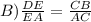`B) (DE )/(EA) =(CB)/(AC)` TRUE (from 2)

`C) (DE )/(EA) =(AC)/(CB)` FALSE

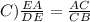`C) (EA)/(DE) =(AC)/(CB)` FALSE